Key words : Schedule, Beta Standard of Deviation, Range of Estimate of Activity Duration (EAD), Range of Estimate of Activity Cost (EAC)
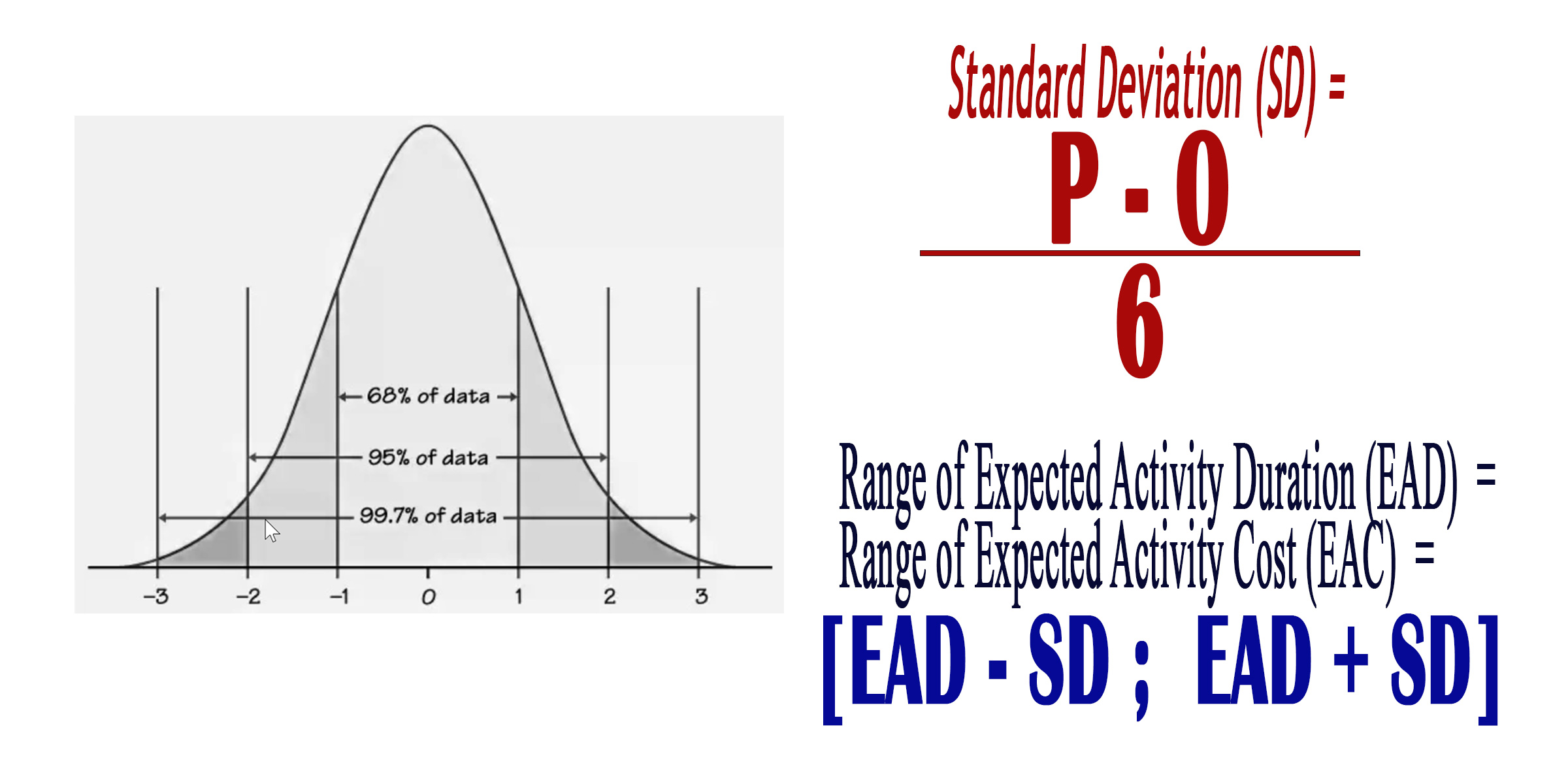
Beta Standard of Deviation (SD)
Beta Standard of Deviation (SD) is measure of how dispersed a group of values are ; It’s the possible range of estimates.
The formula is SD = (P – 0) / 6 where P = Pessimistic and O = Optimistic
Range of Expected Activity Duration
Based on the the value of Standard deviation (SD), we calculate the upper and lower limit values of Expected Activity Duration (or Expected Activity Cost).
Range is the difference of Upper and lower limits
The formula for Range of Expected Activity Duration is :
(EAD – SD , EAD+SD)
The formula for Range of Expected Activity Cost is
(EAC – SD , EAC+SD)
For example, if an activity takes 30 hours to complete with a Standard of Deviation of +/- 5 hours, then the range of Expected Activity of Duration is [30 – 5 ; 30 + 5] = [25 ; 35].
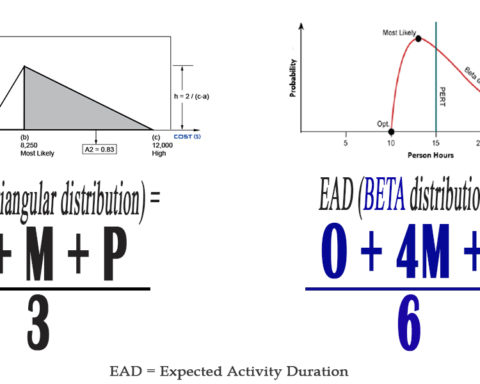
BE CAREFUL : When we calculate here the EAD or the EAC, we use only the Beta distribution only (( P + 4M + O) / 6) and not triangular distribution ((P + M + O) / 3).
KEEP IN MIND : Greater the range, greater is the risk. i.e. as Standard Deviation (SD) increases Risk increases.
Another example : Consider an activity with Optimistic duration estimate of 22 days, a Pessimistic duration estimate of 32 days and a Most likely duration estimate of 26 days. Calculate the Range of estimate.
Solution :
Expected Activity Duration =
= (P + 4M + O) / 6
= (32 + (4*26) + 22) / 6
= (32 + 104 + 22) / 6
= 158 / 6
= 26,33 days
| EAD = 26,33 days |
Standard Deviation =
= (P – O) / 6
= (32 – 22) / 6
= 10 / 6
= 1,67 days
| SD = 1,67 days |
Range of Estimate =
= [EAD – SD ; EAD + SD]
= [26,33 – 1,67 ; 26,33 + 1,67]
= [24,66 ; 28]
|
Range of Estimate = [24,66 ; 28] |